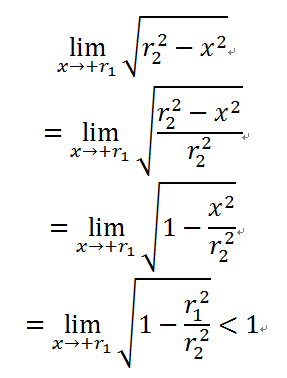ドーナツの穴を残して食べるには?
ドーナツの穴を残して食べるには?
- 皆さんこんばんは。オフィス・宮島です。2ちゃんねるを見てて面白い記事があったので紹介します。
ネット掲示板の「2ちゃんねる」で「ドーナツを穴だけ残して食べる方法」という問いについて考えた有 名な書き込みがある。普通にドーナツを食べたら穴はなくなってしまうが、何とか穴だけを残せないか、と いう疑問への答えを学問領域ごとにシミュレートしてユーモラスに答えたものだ。掲示板でコピー&ペー ストされるたびに改良され、何人もの手で練り上げられた回答が定型文として2ちゃんねるに定着していた。
ところが、2ちゃんねらーの間で広がっていたこの定型文に飽き足らず、アカデミックな立場から真面
目に取り組んだ回答文が新たに公開された。大阪大学の教員・学生らによるもので、書籍として刊行された。
12人の教員が難問に挑む
「ドーナツを穴だけ残して食べる方法」の回答は、2ちゃんねるでは以下のような内容で定着していた。
数学派-非ユークリッド幾何学的には可能(難しいよ派)
化学派-穴に空気とは違う気体をつめれば?(それ残ってるのその気体じゃん派)
統計派-100万回食べれば1回くらい穴だけ残ってるかもしれない(めんどくさいよ派)
言語派-問いかけが漠然としていて厳密な対策が不可能(ごめんなさいだよ派)
このほか延々と学問分野ごとに回答が並び、それらが樹形図のように分類されている。それぞれの学問
分野の回答を短い文で表現し、括弧の中の言葉でオチを付けるというスタイルだ。「分野」や「派閥」を分類 して表記するのは2ちゃんねるで使われる一般的な形式で、似たようなものとして清純アイドルが排便しない という「幻想」をめぐる議論を記したものもある。
(以下略)
- 皆さんもミスタードーナツとかで食べたことがあるドーナツですが、ドーナツの穴を残して食べるにはどうしたらよいでしょうか?

- 私の回答はこうです。
数学的なアプローチ
- ドーナツを単純な円と考えると、下図に示す形状になります。
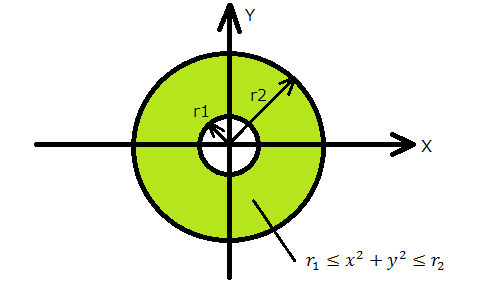
- 穴の半径をr1、ドーナツ部分の半径をr2とすると上に示した式の通りになります。
- ドーナツを食べるときは、「外側から食べる」と仮定すると、このような計算式になります。
- 極限値が0になるときは「ドーナツを全く食べていない」状態で、極限値が1となるときは「ドーナツと穴の径が等しい、即ちドーナツが存在しない」ということになります。
- 先に示した状態を外し、一定量Δrずつ食べてr1に到達したときにドーナツの穴だけが残る…というわけです。
工学的なアプローチ
- 私も一応工学部出身なので、工学的にアプローチしてみようと思います。
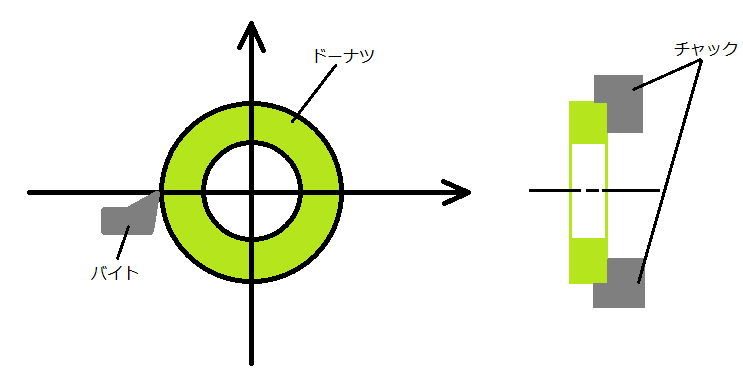
- 下図のようにドーナツを食べるということは汎用旋盤で金属製のドーナツのモデルを削る…という風に定義します。
- バイトと呼ばれる工具を使ってΔrずつ金属を削ってゆくと、ドーナツの直径は2Δrずつ小さくなってゆくのはすぐ想像できると思います。え、想像できない?なぜかというと…旋盤はワークを回転させて削るため、片方をΔr削ったらもう片方もΔr削られるからです。
- このように削ってゆきバイトがr1(穴の位置)に達したとき、そこで材料が消滅します。それを長手方向にも行うとワークそのものが消滅してしまいます。
結論
- 上の結論をまとめると…「数学的には可能だが工学的には無理」ということになります。
- もし、できるとおっしゃる方はこちらまでメールください。これはいいと思ったものにクオカード1000円分を差し上げようと思います。(3月29日18時厳守)
本日はここまでといたします。ご清聴ありがとうございました。