ありがたくないプレゼントの答え
ありがたくないプレゼントの答え
- 皆さんおはようございます。今年ももう残りわずかになりました。オフィス・宮島です。本日は「12月24日に出したありがたくないクリスマスプレゼントの解答」を発表します。
問1
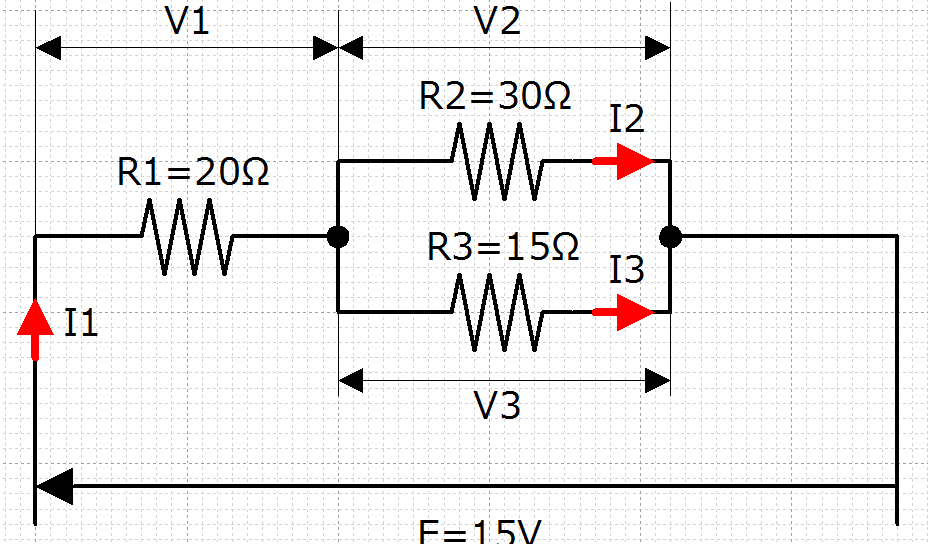
- 下図に示す回路の電流および電圧を求めよ。
- これは直並列回路と呼ばれるものです。まずはR1、R2およびR3にかかる電圧を求めてみましょう。
- R2とR3は並列回路になっていますので、ここの合成抵抗はこのようになります。
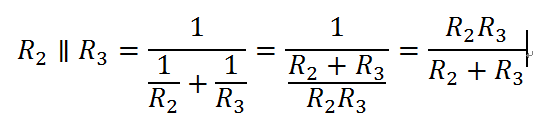
- これを使って計算すると…
R2//R3=(30・15) / (30+15)=450/45=10Ωとなります。これを使って回路全体の抵抗を計算すると、R=20+10=30Ωとなります。
- 各抵抗にかかる電圧は…
V1=I・R1=0.5×20=10V
V2'=I・R2//R3=0.5×10=5Vとなり、R2とR3は並列回路であるから、V2'=V2=V3となるので、∴V2=V3=5Vとなります。
- 回路に流れる電流は…
I1 = E/Rであるから、15/30=0.5A
I2 = V2 / R2 = 5 / 30=0.166…≒0.167A
I3 = V2(V3) / R3 = 5 /15=0.333…≒0.333Aとなります。
問2
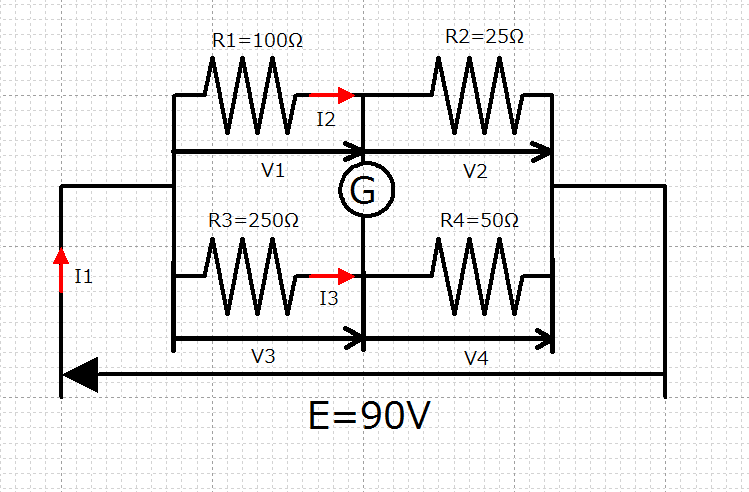
- 次に示す回路の抵抗にかかる電圧・電流を求めよ。
- これも直並列回路です。今度はR1とR2が直列、R3とR4が直列で、R1とR2、R3とR4が並列になっているタイプです。
- 並列回路の特性から、R1とR2の組には90Vの電圧がかかり、R3とR4の組にも90Vの電圧がかかります。それを利用してR1とR2の組およびR3とR4の組にかかる電流を計算します。
- 電流・電圧を計算すると…
電流は…
I2 = E / (R1+R2) = 90/(100+25)=0.72A
I3 = E / (R1+R2) = 90/(250+50)=0.3Aより
∴I1=I2+I3であるから、I1=0.72+0.3=1.03Aとなります。
各抵抗にかかる電圧は…
V1 = I2・R1 = 0.72×100=72V
V2 = I2・R2 = 0.72×25=18V
V3 = I3・R3 = 0.3×250=75V
V4 = I3・R4 = 0.3×50=15V…となります。
- 次に、この回路は直並列回路の中でも特別なタイプで、このような回路を特にブリッジ回路といいます。ブリッジ回路にて次に示すように抵抗を設定すると、検流計に電流が全く流れなくなります。
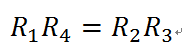
- これを利用して抵抗を正確かつ精密に測定します。(おわり)
今回は応募者がゼロだったので、プレゼントはありません。